1/ Giới thiệu về biến ngẫu nhiên
Trong xác suất thống kê, một biến ngẫu nhiên (random variable, stochastic variable) là một hàm toán học với đặc điểm: nó gán một giá trị bằng số cho kết quả (đầu ra) của một phép thử ngẫu nhiên (thực nghiệm).

Định nghĩa:
Một biến ngẫu nhiên là một hàm: X : Ω → R
Hay nói một cách khác gán mỗi kết quả ω bằng một con số thực X(ω).
Nhờ vào định nghĩa của biến ngẫu nhiên, mà từ đó ta có thể làm nhiều phép toán khác nhau với các biến ngẫu nhiên: cộng, trừ, nhân, chia,… Từ đó có thể sinh ra các biến ngẫu nhiên mới từ các biến ngẫu nhiên cho trước.
Ví dụ 1: Giải nhất trong bảng kết quả xsmn thứ 3 là một biến ngẫu nhiên với nhiều dãy số khác nhau có thể xuất hiện.
Ví dụ 2: Tung đồng xu (Sấp – S, Ngửa – N) lên 6 lần. Gọi X(ω) là số lần sấp của ω. Kết quả ω = SSSNSN ta có X(ω) = 4.
Biến ngẫu nhiên được phân ra làm hai loại: biến ngẫu nhiên rời rạc, biến ngẫu nhiên liên tục.
2. Phân phối xác suất
Là phương pháp xác định xác suất của biến ngẫu nhiên được phân phối ra sao. Có 2 cách để xác định phân bố này là dựa vào bảng phân bố xác suất và hàm phân phối xác suất. Ở đây, tôi chỉ đề cập tới phương pháp hàm phân bố xác suất. Hàm phân phối xác suất của biến ngẫu nhiên XX được xác định như sau:
![]()
Hàm phân phối xác suất còn có tên là hàm phân phối tích lũy (CDF – Cumulative Distribution Function) do đặc trưng là lấy xác suất của các biến ngẫu nhiên bên trái của một giá trị x bất kì nào đó. Hàm này có đặc điểm là một hàm không giảm, tức là nếu a < b thì vì sự kiện b đã bao gồm cả sự kiện a rồi.

2.1 Hàm khối xác suất của biến rời rạc
Với các biến ngẫu nhiên ta còn quan tâm xem xác suất tại mỗi tại 1 giá trị x nào đó trong miền giá trị của nó là bao nhiêu, hàm xác suất như vậy đối với biến ngẫu nhiên rời rạc được gọi là hàm khối xác suất (PMF – Probability Mass Function). Giả sử miền xác định của X là D, tức X:Ω↦D thì hàm khối xác suất được xác định như sau:

Như vậy ta có thể thấy rằng hàm khối xác suất thực chất cũng là một xác suất nên nó mang đầy đủ tất cả các tính chất của xác suất như:

2.2. Hàm mật độ xác suất của biến liên tục
Với các biến ngẫu nhiên liên tục ta có khái niệm hàm mật độ xác suất (PDF – Probability Density Function) để ước lượng độ tập trung xác suất tại lân cận điểm nào đó. Hàm mật độ xác suất f(x) tại điểm x được xác định bằng cách lấy đạo hàm của hàm phân phối tích lũy F(x) tại điểm đó:
![]()
Như vậy thì nơi nào f(x) càng lớn thì ở đó mức độ tập xác suất càng cao. Từ đây ta cũng có thể biểu diễn hàm phân phối tích lũy như sau:

Xác suất trong 1 khoảng (α,β) cũng có thể được tính bằng hàm mật độ xác suất:
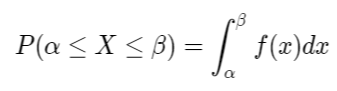
Hàm mật độ xác suất cũng có 2 tính chất như xác suất như sau:

Hiện nay, việc chú trọng giảng dạy và nghiên cứu các vấn đề liên quan đến toán học rời rạc ngày càng ứng dụng rộng rãi và mạnh mẽ hơn trước nhờ sự phổ biến của máy tính tốc độ cao. Một ví đơn giản trong việc quay thử kết quả xo so vung tau. Bảng kết quả gồm 9 giải từ giải 8 đến đặc biệt. Mỗi giải lại được cấu tạo gồm các chữ số khác nhau. Suy ra biến ngẫu nhiên của chúng khác nhau. Con người không thể tính toán hết tất cả các trường hợp xuất hiện của các giải nhưng máy tính thì có thể. Nó giúp bạn tìm ra các dãy số ngẫu nhiên nhanh chóng.

